Even Scientists Can Be Fooled Twice!


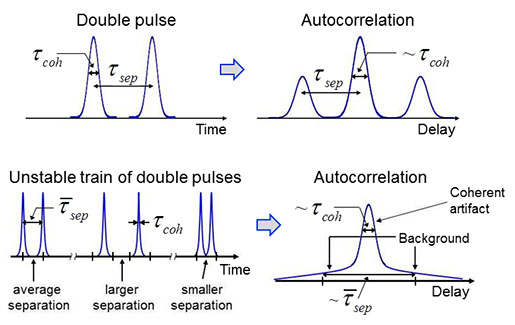
The coherent artifact in autocorrelation. Top: Double pulse and its autocorrelation. Bottom: A train of variably spaced double pulses and their multi-shot autocorrelation (averaged over many pulses in the train). The coherent artifact results from the short nonrandom coherent component of the double pulses (specifically, a single pulse), while the broader background results from the overall average pulse length (the combination of both pulses). This trace is typical of autocorrelations of nearly all trains of unstable complex pulses.

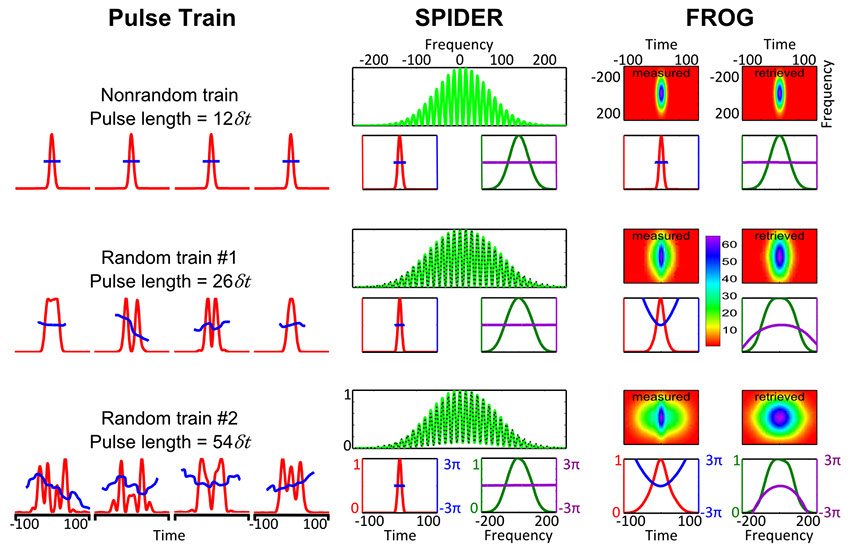
Nonrandom- and random-pulse trains of varying complexity, and simulated multi-shot SPIDER and SHG FROG measurements of them. Top row: nonrandom train of identical Gaussian flat-phase pulses. Middle and bottom rows: random-pulse trains of different average complexity and duration. Red curves indicate intensity, blue phase, green spectrum, and purple spectral phase. The black dotted SPIDER traces are fits assuming flat-phase Gaussian pulses and slight misalignment of the SPIDER device (unequal intensities of the two pulses in it), confirming that a stable train of short pulses and an unstable train of longer pulses cannot be distinguished by SPIDER. For all three pulse trains, SPIDER retrieves only the nonrandom pulse component and exhibits decreasing fringe visibility (100%, 98%, and 90%, respectively). In short, SPIDER only measures the coherent artifact. As a result, it probably cannot be used to measure pulse lengths. FROG also does not see the pulse structure, but it does yield the correct durations. More importantly, in FROG, the measured and retrieved FROG traces disagree for the random trains, and their rms differences are large. This is the key: such disagreement is the indication that instability is present.
To summarize, we find that SPIDER retrieves an excellent estimate of only the nonrandom component of the pulse train. But it does not see any randomly varying component of the pulse. It also cannot see unstable double-pulsing. In short, for an unstable pulse train, multi-shot SPIDER measures only the coherent artifact.
This should not be surprising: it's been known for over 200 years that interferometric methods (of which SPIDER is one), in general, are not sensitive to random phase variations, responding only with reduced fringe visibility and increased background. The same holds for other interferometric methods.
Alas, we are unaware of any SPIDER measurements with fringe visibilities greater than 98%, a value that, in our simulations, corresponds to a measured pulse length too short by more than a factor of 2. Indeed, in supercontinuum measurements, much smaller values—as low as 10%—have been reported. Without deeper insight into the underlying physics or additional independent measurements, it appears impossible to determine whether an imperfect SPIDER fringe visibility is due to benign misalignment effects (and so corresponds to a stable train of short pulses) or instability (and so corresponds to an unstable train of potentially much longer ones). Thus, unless the pulse-to-pulse stability of the temporal intensity can otherwise be ensured (which is currently not possible unless a FROG measurement is made), it appears that pulse-length claims from measurements with imperfect SPIDER fringe visibility require re-evaluation.
So how did some of the brightest scientists in the world make the same mistake twice? Perhaps it was wishful thinking: every ultrafast scientist likes to be able to brag about having extremely short pulses, and SPIDER routinely gives shorter pulses than other methods do, as our results have shown.
Actually, some FROG measurements will also require re-evaluation. While FROG yields the correct pulse lengths in our simulations, it, like SPIDER, misses the pulse structure and so could also yield misleading results in the presence of instability. However, FROG provides a strong indicator of instability: disagreement between the measured and retrieved FROG traces. Unfortunately, some authors have incorrectly attributed such disagreement to possible non-convergence of the FROG algorithm. In view of our results and the FROG algorithm’s demonstrated robustness for all but extremely complex pulses, such discrepancies are essentially always due to instability. Fortunately, instability is often considered as the cause, having previously been encountered experimentally in FROG measurements of supercontinuum pulse trains. In that case, FROG retrieved a pulse with the extreme complexity of a typical pulse in the train, and it was the disagreement between the measured and retrieved traces that indicated a problem and inspired single-shot spectral measurements and extensive theoretical investigations, confirming the highly unstable nature of the continuum.
In any case, pulse trains should be considered guilty of instability until proven innocent. Also, in FROG measurements, retrieved traces should always be reported. Only good agreement between measured and retrieved FROG traces or a 100% SPIDER fringe visibility (which is very difficult to achieve) can imply good pulse-train stability.
Worse, in more recent work, we're finding that essentially all other techniques (except for FROG and GRENOUILLE) have the same problem as SPIDER. So be careful how you measure your pulses!
Read more in our short paper on the subject (Ratner, et al.) or our longer one (Rhodes, et al.).
And for more detailed information, click on our Prose page, and check out all the Rhodes, et al., papers.
