Pulse Compression
Most ultrashort laser pulses pass through glass or other materials on their way to their final destination, which lengthens the pulse and introduces positive chirp into the pulse (the red precedes the blue). The well-known prism (or grating) pulse compressor compensates for this effect, reducing the pulse length to its original and eliminating the chirp.
It's based on the fact that angular dispersion introduces negative chirp. But angular dispersion also introduces other spatio-temporal distortions, so three additional prisms are required to compensate for them.


How do you operate a pulse compressor? You vary the chirp (GDD) by moving any prism into or out of the beam, introducing more or less glass (positive chirp). Or you can change the separation between the 1st and 2nd prisms (and also the 3rd and 4th prisms, maintaining these two distances equal). Changing your pulse's wavelength requires tilting all four prisms by the same amount.
Needless to say, that's way too complicated. So the two-prism compressor was invented to simplify it. But it's still complex, and maintaining its alignment when the laser beam into it wanders even slightly is a pain.
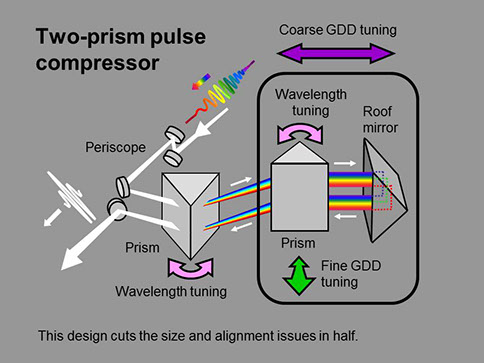
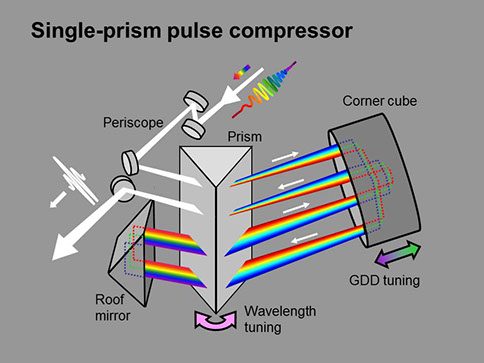
So we invented a single-prism pulse compressor (Akturk, et al.), which takes advantage of the precision of corner cubes, which retro-reflect a pulse parallel to its incident direction to within a few arcseconds. This device is much easier to work with: a single knob changes the chirp and another changes the wavelength. Also, it cannot be misaligned, and it cannot introduce any spatio-temporal distortions!
Even better, you can place two or three prisms in it (the achievable negative GDD will be 4 or 9 times that of a single-prism device). Or you can place a grating and a prism (Chauhan, et al.) in it for even more GDD. This also provides the ability to compensate for higher-order dispersion. All without the need for careful alignment.
Also, modeling the dispersion of this device wouldn't have been possible without a very nice, elegant equation we derived (Chauhan and Trebino) for the total dispersion of an arbitrary number of dispersive elements of any kind.
