SEA TADPOLE with Phase Diversity Measures Pulses Completely in Space and Time!
The ultimate goal of optical measurement technology is the measurement of the complete spatio-temporal field of light, E(x,y,z,t). Unfortunately, measuring separate pulse and beam shapes is insufficient, as even common optical elements, such as prisms and lenses, introduce spatiotemporal distortions, in which the temporal field depends on position. These effects necessitate the measurement of the complete spatio-temporal field, E(x,y,z,t), often with submicron spatial resolution and fs temporal resolution. To solve this problem, we recently introduced a measurement technique called scanning SEA TADPOLE, which can, in principle, measure the complete four-dimensional electric field, E(x,y,z,t) of ultrashort pulses with the required spatial and temporal resolutions.
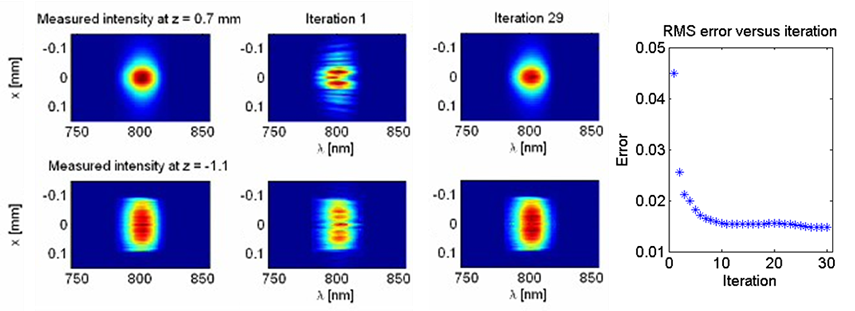
Spatial-phase retrieval results. First column: Measured spatio-spectral amplitudes at z1 (top) and z2 (bottom). Second column: Spatio-spectral intensities obtained by propagating the field at z2 to z1 (top) and vice versa (bottom) using the measured spatial phase after only one iteration. Third column: Same as the previous, but using the retrieved spatial phase after 29 iterations. Note the excellent agreement between the first and last columns.
SEA TADPOLE has spatial resolution approximately equal to the mode size of its fiber, which can be as small as 50nm, as demonstrated by Pam Bowlan (Bowlan, et al.). In order to measure the spatial dependence of the field, the fiber is scanned in the transverse and longitudinal (propagation) directions, so that E(x,y,z,w), where w is the frequency, is measured at each fiber position (x,y,z), and, as a result, the complete spatiotemporal field E(x,y,z,w) is obtained. This quantity can be Fourier transformed to yield the complete field versus space and time E(x,y,z,t). However, SEA TADPOLE uses a fiber interferometer, so it is afflicted with a slow phase drift (about 1rad/s) due to the inherent difficulty of maintaining optics to the required submicron accuracies while scanning them and also due to small refractive-index changes in the fibers. Thus, a measurement of E(x,y,w), which can require a minute or more, randomizes the spatial phase, that is, the zeroth-order spectral-phase coefficient vs. transverse position in the expansion of the spectral phase vs. frequency. But using SEA TADPOLE measurements of the field at just two planes, in conjunction with a phase diversity algorithm, Pam has shown in a recent paper that we can, not only obtain the true spatial phase, but also obtain the complete spatio-temporal field at all planes, that is, all points in space.

Measured (top) and numerically propagated spatio-spectral intensities using the field from z = −1.1mm, including the retrieved spatial phase.
